At the University of Rostock, researchers have combined PT symmetry with topology in photonic chips, challenging previous beliefs about open systems and topological insulators, and paving the way for innovative technological applications. Credit: SciTechDaily.com
Groundbreaking research merges PT symmetry with topology, offering new insights into open systems and the potential for advanced technological circuits.
Whether describing the orbits of planets or the inner workings of the atom, a key paradigm in physics is the conservation of energy: While different forms of energy may be converted into one another, the total amount of energy is typically assumed to be constant over time. Therefore, physicists usually tend to make sure that the system they are trying to describe does not interact with its environment.
Yet, as it turns out, the dynamics of a system can also be stable if the gain and loss of energy are distributed in a systematic fashion such that they cancel each other out under all conceivable conditions, which can be ensured by so-called parity time (PT) symmetry: Similar to a video that is played backward and simultaneously is reflected in a mirror and yet looks exactly like the original video – i.e., is PT-symmetrical – the components in the system are arranged in such a way that an exchange of gain and loss of light through the simultaneous mirroring and time reversal. makes the system appear unchanged. Far from being a purely academic notion, PT symmetry has paved the way for a deeper understanding of open systems.

A research team from Rostock, Würzburg and Indiana has shown for the first time that light can propagate without loss in systems that interact with their environment. For their experiments, they used laser-written waveguides as shown here – these are optical structures written into a material by a laser beam. Here, the light signal can propagate robustly and stably and without losses Credit: Julia Tetzke/University of Rostock
Innovations With PT Symmetry
The fascinating physical phenomena associated with PT symmetry are the specialty of Professor Alexander Szameit at the University of Rostock. In their custom photonic chips, laser light can mimic the behavior of natural and synthetic materials, that are arranged in periodic lattice structures, alike, making them an ideal testbed for a large variety of physical theories.
In this way, Professor Szameit and his team have managed to combine PT symmetry with the concept of topology. Topology studies properties that do not change despite the underlying system being continuously deformed. Such properties then make a system particularly robust against external influences.
For their experiments, Szameit’s research group uses laser-inscribed photonic waveguides – optical structures written into a material by a laser beam. In these “circuits for light,” so-called topological insulators are realized. Szameit explains: “These insulators have attracted a lot of attention in recent years because of their fascinating ability to convey a lossless stream of electrons or light along their boundary. The unique capability to suppress the impact of defects and scattering makes them particularly interesting for all kinds of technological applications.”
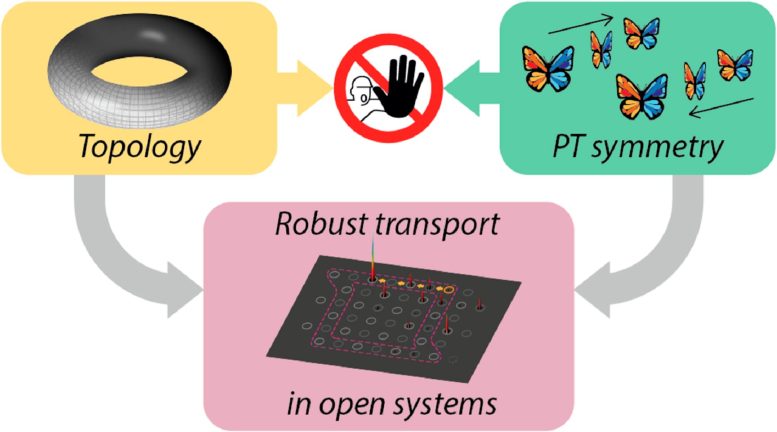
Topology meets open systems: Topology is concerned with the invariable properties of systems – as shown schematically in the yellow figure above left with the donut-like structure, whose number of holes, namely exact one hole, always remains the same. On the other hand, parity-time symmetry – illustrated by the motion of a butterfly that looks the same if reversed and mirrored – plays an important role in the stability of open systems. Combining these two concepts has long been a problem for researchers, as they seemed incompatible. However, researchers could now show that the movement of a light signal (yellow dots and peak at the end of the red marker) moves robustly and stably along the edge of a laser-written waveguide despite interacting with its environment (bottom image). Credit: Alexander Fritzsche/University of Rostock
New Discoveries in Topological Insulators and Open Systems
However, until now, such robust boundary states were thought to be fundamentally incompatible with open systems. In their joint effort, the researchers from Rostock, Würzburg, and Indianapolis were able to show that the apparent paradox can be resolved by dynamically distributing gain and loss over time.
The first author, PhD student Alexander Fritzsche, elaborates: “The light propagating along the boundary of our open system is like a hiker traversing mountainous terrain. Despite all the ups and downs, they will inevitably end up back at the initial elevation of the starting point. Similarly, the light propagating within the protected edge channel of our PT-symmetric topological insulator will never be exclusively amplified or damped, and can therefore retain its average amplitude while enjoying the full robustness afforded of the topology.”
These findings are an important contribution to the fundamental understanding of topological insulators and open systems, and may open the gates to a new generation of advanced circuits for electricity, light or even sound waves.
Reference: “Parity–time-symmetric photonic topological insulator” by Alexander Fritzsche, Tobias Biesenthal, Lukas J. Maczewsky, Karo Becker, Max Ehrhardt, Matthias Heinrich, Ronny Thomale, Yogesh N. Joglekar and Alexander Szameit, 9 January 2024, Nature Materials.
DOI: 10.1038/s41563-023-01773-0
This research was funded by the German Research Foundation (DFG) and supported by the Alfried Krupp von Bohlen und Halbach Foundation.





