Quantum bits can be described more precisely with the help of newly discovered harmonics as a team of 30 researchers reports in Nature Physics.
Physicists have uncovered that Josephson tunnel junctions – the fundamental building blocks of superconducting quantum computers – are more complex than previously thought. Just like overtones in a musical instrument, harmonics are superimposed on the fundamental mode. As a consequence, corrections may lead to quantum bits that are 2 to 7 times more stable. The researchers support their findings with experimental evidence from multiple laboratories across the globe, including the University of Cologne, Ecole Normale Supérieure in Paris, and IBM Quantum in New York.
A Collaborative Breakthrough
It all started in 2019, when Dennis Willsch and Dennis Rieger – two PhD students from FZJ and KIT at the time and joint first authors of the paper – were having a hard time understanding their experiments using the standard model for Josephson tunnel junctions. This model won Brian Josephson the Nobel Prize in Physics in 1973.
Excited to get to the bottom of this, the team led by Ioan Pop scrutinized further data from the Ecole Normale Supérieure in Paris and a 27-qubit device at IBM Quantum in New York, as well as data from previously published experiments. Independently, researchers from the University of Cologne observed similar deviations of their data from the standard model.
“Fortunately, Gianluigi Catelani, who was involved in both projects and realized the overlap, brought the research teams together!” recalls Dennis Willsch from FZ Jülich. “The timing was perfect,” adds Chris Dickel from the University of Cologne, “since, at that time, we were exploring quite different consequences of the same underlying problem.”
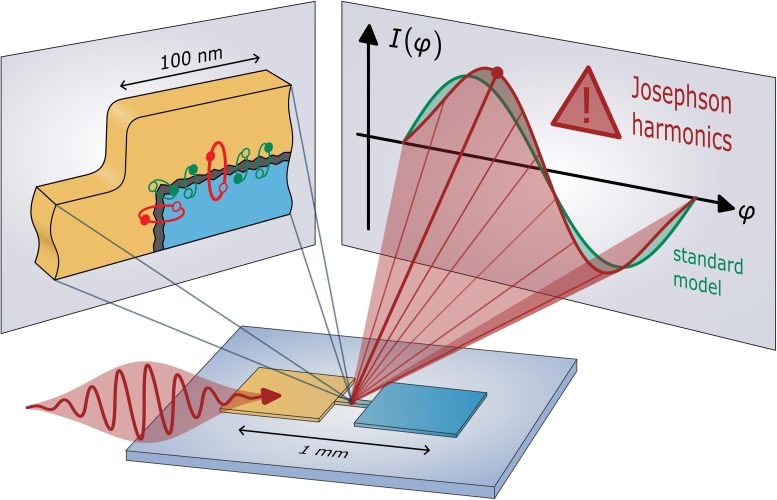
Bottom part: By exciting superconducting circuits (yellow/blue) with microwave signals (red wiggly arrow), the researchers can analyze the fundamental equation that describes the Josephson tunnel junction of the circuit. Right part: The researches have observed significant deviations (red curve) from the sinusoidal standard model (green curve). Left part: schematic zoom-in of a tunnel junction consisting of two superconductors (yellow/blue) with a thin insulating barrier in-between. The large conduction channels (red loops) can be responsible for the observed deviations from the standard model. Credit: Dennis Rieger, Patrick Winkel
Harmonics in Quantum Bits
Josephson tunnel junctions consist of two superconductors with a thin insulating barrier in between and, for decades, these circuit elements have been described with a simple sinusoidal model.
However, as the researchers demonstrate, this “standard model” fails to fully describe the Josephson junctions that are used to build quantum bits. Instead, an extended model including higher harmonics is required to describe the tunneling current between the two superconductors. The principle can also be found in the field of music. When the string of an instrument is struck, the fundamental frequency is overlaid by several harmonic overtones.
“It’s exciting that the measurements in the community have reached the level of accuracy at which we can resolve these small corrections to a model that has been considered sufficient for more than 15 years,” Dennis Rieger remarks.
Implications for Quantum Computing
When the four coordinating professors – Ioan Pop from KIT and Gianluigi Catelani, Kristel Michielsen, and David DiVincenzo from FZJ – realized the impact of the findings, they brought together the large collaboration of experimentalists, theoreticians, and material scientists, to join their efforts in presenting a compelling case for the Josephson harmonics model. In the Nature Physics publication, the researchers explore the origin and consequences of Josephson harmonics.
“As an immediate consequence, we believe that Josephson harmonics will help in engineering better and more reliable quantum bits by reducing errors up to an order of magnitude, which brings us one step closer towards the dream of a fully universal superconducting quantum computer,” the two first authors conclude.
Reference: “Observation of Josephson harmonics in tunnel junctions” by Dennis Willsch, Dennis Rieger, Patrick Winkel, Madita Willsch, Christian Dickel, Jonas Krause, Yoichi Ando, Raphaël Lescanne, Zaki Leghtas, Nicholas T. Bronn, Pratiti Deb, Olivia Lanes, Zlatko K. Minev, Benedikt Dennig, Simon Geisert, Simon Günzler, Sören Ihssen, Patrick Paluch, Thomas Reisinger, Roudy Hanna, Jin Hee Bae, Peter Schüffelgen, Detlev Grützmacher, Luiza Buimaga-Iarinca, Cristian Morari, Wolfgang Wernsdorfer, David P. DiVincenzo, Kristel Michielsen, Gianluigi Catelani and Ioan M. Pop, 14 February 2024, Nature Physics.
DOI: 10.1038/s41567-024-02400-8